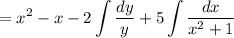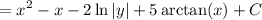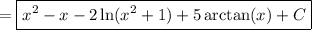Question

∫(2x^3-x^2-2x+4)/(1+x^2)dx

Answer 1

Simplify the integrand as

`(2x^3 - x^2 - 2x + 4)/(1 + x^2) = ((2x^3 + 2x) - (x^2 + 1) - 4x + 5)/(x^2 + 1) \\\\ = (2x(x^2 + 1) - (x^2 + 1) - 4x + 5)/(x^2 + 1) \\\\ = 2x - 1 - (4x - 5)/(x^2 + 1)`

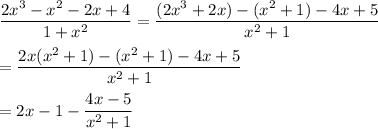
(in other words, compute the quotient and remainder)

We can further split up and prepare the remainder term for integration by rewriting it as

`(4x - 5)/(x^2 + 1) = 2*(2x)/(x^2 + 1) - \frac5{x^2 + 1}`

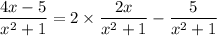
Now we integrate:

`\displaystyle (2x^3 - x^2 - 2x + 4)/(1 + x^2) \, dx = \int \left(2x - 1 - 2*(2x)/(x^2+1) + \frac5{x^2+1}\right) \, dx`

`\displaystyle = x^2 - x - 2 \int (2x)/(x^2+1) \, dx + 5 \int (dx)/(x^2+1)`

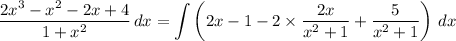
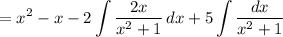
In the first remaining integral, substitute y = x² + 1 and dy = 2x dx. In the last integral, recall that d/dx [arctan(x)] = 1/(x² + 1).

`\displaystyle = x^2 - x - 2 \int \frac{dy}y + 5 \int (dx)/(x^2+1)`

`\displaystyle = x^2 - x - 2 \ln|y| + 5 \arctan(x) + C`

`\displaystyle = \boxed{x^2 - x - 2 \ln(x^2+1) + 5 \arctan(x) + C}`