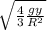Answer:
w =
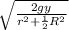
Step-by-step explanation:
For this exercise let's start by applying Newton's second law to the mass with the string
W - T = m a
In this case, as the system is going down, we will assume the vertical directional down as positive.
T = W - m a
Now we apply Newton's second law for rotational motion to the pulley of radius r. We will assume the positive counterclockwise rotations
∑ τ = I α
T r = I α
the moment of inertia of the disk is
I = ½ M R²
angular and linear acceleration are related
a = α r
we substitute
T r = (½ m R²) (a / r)
T = ½ m (
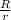 )² a
)² a
we write our two equations
T = W - m a
T = ½ m (
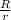 )² a
)² a
we solve the system of equations
W - m a = ½ m (\frac{R}{r} )² a
m g = m a [ 1 + ½ (\frac{R}{r} )² ]
a =
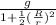
this acceleration is constant throughout the trajectory, so with the angular and lineal kinematics relations
w² = w₀² + 2 α θ
v² = v₀² + 2 a y
as the system is released its initial angular velocity is zero
w² = 0 + 2 α θ
v² = 0 + 2 a y
we look for the angular acceleration
a =α r
α = a / r
α =
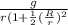
we look for the angle, remember that they must be measured in radians
θ = s / r
in this case we approximate the arc to the distance
s = y
θ = y / r
we substitute
w =
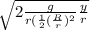
w =
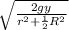
for the simple case where r = R
w =
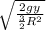
w =