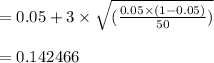Question

You are working in a small, student-run company that sends out merchandise with university branding to alumni around the world. Every day, you take a sample of 50 shipments that are ready to be shipped to the alumni and inspect them for correctness. Across all days, the average percentage of incorrect shipments is 5 percent. What would be the upper control limit for a p-chart

Answer 1

The answer is "0.142466".

Explanation:

Using the p formula for the proportion of nonconforming units through the subgrouping which can vary in sizes:

`p =(np)/(n)\\\\`

`\bar{p}=(\Sigma np)/(\Sigma n)\\\\`

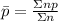
Defects
`= (5)/(100) * 50 \\\\`

`p = (5)/(100) * (50)/(50)=0.05\\\\`

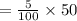
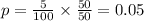
It calculates the controls limits through the p-chart that is:

`UCL_(p),LCL_(p)=\bar{p} \pm \sqrt{\frac{\bar{p}(1-\bar{p})}{\bar{n}}}\\\\`

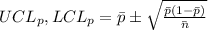
So, the upper control limits:

`= 0.05 + 3 * \sqrt{((0.05*(1-0.05))/(50))} \\\\= 0.142466`