Question

According to the U.S. Census Bureau, 11% of children in the United States lived with at least one grandparent in 2009 (USA TODAY, June 30, 2011). Suppose that in a recent sample of 1550 children, 214 were found to be living with at least one grandparent. At a 2% significance level, can you conclude that the proportion of all children in the United States who currently live with at least one grandparent is higher than 11%

Answer 1

The pvalue of the test is 0.0001 < 0.02, which means that we reject the null hypothesis and accept the alternate hypohteis that the proportion of all children in the United States who currently live with at least one grandparent is higher than 11%.

Explanation:

Proportion of all children in the United States who currently live with at least one grandparent is higher than 11%

This means that the null hypothesis is:

`H_0: p = 0.11`

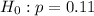
And the alternate hypothesis is:

`H_a: p > 0.11`

The test statistic is:

`z = (X - \mu)/((\sigma)/(√(n)))`

In which X is the sample mean,
`\mu` is the value tested at the null hypothesis,
`\sigma` is the standard deviation and n is the size of the sample.

0.11 is tested at the null hypothesis:

This means that
`\mu = 0.11, \sigma = √(0.11*0.89)`

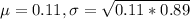
Suppose that in a recent sample of 1550 children, 214 were found to be living with at least one grandparent.

This means that:

`n = 1550, X = (214)/(1550) = 0.1381`

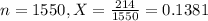
Value of the test statistic:

`z = (X - \mu)/((\sigma)/(√(n)))`

`z = (0.1381 - 0.11)/((√(0.11*0.89))/(√(1550)))`

`z = 3.54`

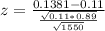
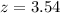
Pvalue of the test and decision:

This is the probability of finding a sample proportion above 0.1381, which is 1 subtracted by the pvalue of Z = 3.54.

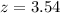`z = 3.54` has a pvalue of 0.9999

1 - 0.9999 = 0.0001

The pvalue of the test is 0.0001 < 0.02, which means that we reject the null hypothesis and accept the alternate hypohteis that the proportion of all children in the United States who currently live with at least one grandparent is higher than 11%.