Question

The drag Prevnar is a vaccine meant to prevent meningitis. It is typically administered to infants between 12 and 15 months of age. Of the 710 infants,121 experienced a loss of appetite. Is there significant evidence to conclude the proportion of infants who receive Prevnar and experience of a loss of appetite is different from 0.135, the proportion of children who experience a loss of appetite with competing medications? Use α=0.01 level of significance.

Answer 1

The pvalue of the test is 0.0058 < 0.01, which means that there is significant evidence to conclude the proportion of infants who receive Prevnar and experience of a loss of appetite is different from 0.135.

Explanation:

Test if the proportion of infants who receive Prevnar and experience of a loss of appetite is different from 0.135

This means that the null hypothesis is:

`H_(0): p = 0.135`

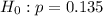
And the alternate hypothesis is:

`H_(a): p \\eq 0.135`

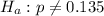
The test statistic is:

`z = (X - \mu)/((\sigma)/(√(n)))`

In which X is the sample mean,
`\mu` is the value tested at the null hypothesis,
`\sigma` is the standard deviation and n is the size of the sample.

0.135 is tested at the null hypothesis:

This means that
`\mu = 0.135, \sigma = √(0.135*0.865)`

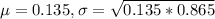
Of the 710 infants,121 experienced a loss of appetite.

This means that
`n = 710, X = (121)/(710) = 0.1704`

Value of the test-statistic:

`z = (X - \mu)/((\sigma)/(√(n)))`

`z = (0.1704 - 0.135)/((√(0.135*0.865))/(√(710)))`

`z = 2.76`

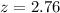
Pvalue of the test and decision:

The pvalue of the test is the pobability that the population proportion differs from the tested proportion by at least 0.1704 - 0.135 = 0.0354, which is P(|z| > 2.76). This probability is 2 multiplied by the pvalue of z = -2.76.

Looking at the z-table, z = -2.76 has a pvalue of 0.0029

2*0.0029 = 0.0058

The pvalue of the test is 0.0058 < 0.01, which means that there is significant evidence to conclude the proportion of infants who receive Prevnar and experience of a loss of appetite is different from 0.135.