9514 1404 393
Answer:
Q ≈ 0.0314148930589 radians ≈ 1.79994078613°
Explanation:
There is no algebraic solution for the set of equations with mixed polynomial and trig functions:
x·sin(Q/2) = 5
1/2x^2(Q -sin(Q)) = π/12
__
However, we can use the first equation to substitute for x in the second equation. This gives ...

This can be simplified using the half-angle identity and recast as a function of Q:
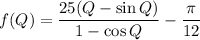
This function will have a zero at the desired value of Q. It can be solved iteratively. A graph shows an approximate value of Q is 0.314 (radians). The value can be refined by Newton's method iteration to give the angle to full calculator precision:
Q ≈ 0.0314148930589 radians ≈ 1.79994078613°
__
The corresponding value of x is about 318.333447755. In short, this is a very narrow sector/segment in a relatively large circle.