Question

1. A recent survey found that 64.7% of the population own their homes. In a random sample of 150 heads of households, 92 responded that they owned their homes. At the 0.01 level of significance, does that indicate a difference from the national proportion?

Answer 1

Given :

Possible chances, x = 92

Sample size, n = 150

Success rate,
`$p=(x)/(n)$`

`$=(92)/(150)=0.6133$`

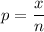
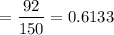
Success probability,
`$p_o$` = 0.647

Failure probability,
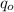`$q_o$` = 0.353

The null hypothesis,
`$H_o:p=0.647$`

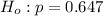
The alternate hypothesis,
`$H_1:p!=0.647$`

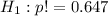
Level of significance, α = 0.01

Therefore from the standard table, the two tailed z = α/2 = 2.576

Since the test is a two tailed test,

we reject the null hypothesis, i.e.
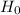`$H_0$`, if
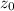`$z_0$` < - 2.576 or if
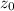`$z_0$` > 2.576

We use the test statistics z proportion =
`$\frac{p-p_0}{\sqrt{(p_oq_o)/(n)}}$`

`$z_o=\frac{0.61333-0.647}{\sqrt{(0.228391)/(150)}}$`

`$z_o=-0.8628$`

`$|z_o|=0.8628$`

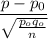
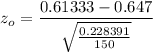
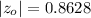
The critical value,

The value of |
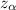`$z_(\alpha)$` | at los 0.01% is 2.576

So we got,
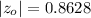`$|z_o|=0.8628$` and |
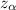`$z_(\alpha)$` | = 2.576

Conclusion :

Therefore, the value of
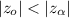`$|z_o|<|z_(\alpha)|$` and here we do not reject the
`$H_0$`

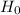
The p-value : two tailed -
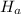`$H_a$` : (p! = -0.86279) = 0.38825

Hence the value of p(0.01) < 0.3883, so here we do not reject the
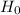`$H_0$`.