Question

Bt= 8500 *(8/27)^t/3After a special medicine is introduced into a Petri dish full of bacteria, the number of bacteria remaining in the dish decreases rapidly.

Answer 1

Every 1.71 seconds, the bacteria loses
`(1)/(2)`

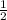
Explanation:

Given

`B(t) = 8500 * ((8)/(27))^(t)/(3)\\`

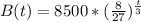
Required [Missing from the question]

Every __ seconds, the bacteria loses
`(1)/(2)`

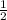
First, we model the function from t/3 to t.

`B(t) = 8500 * ((8)/(27))^(t)/(3)\\`

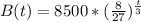
Apply law of indices

`B(t) = 8500 * ((8^(1)/(3))/(27^(1)/(3)))^t`

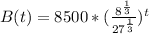
Evaluate each exponent

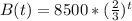`B(t) = 8500 * ((2)/(3))^t` --- This gives the number of bacteria at time t

At time 0, we have:

`B(0) = 8500 * ((2)/(3))^0`

`B(0) = 8500 * 1`

`B(0) = 8500`

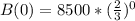
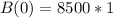
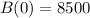
Let r be the time 1/2 disappears.

When 1/2 disappears, we have:

`B(r) = (B(0))/(2)`

`B(r) = (8500)/(2)`

`B(r) = 4250`

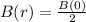
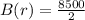
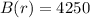
So, we have:

`B(t) = 8500 * ((2)/(3))^t`

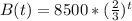
Substitute r for t

`B(r) = 8500 * ((2)/(3))^r`

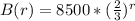
Substitute
`B(r) = 4250`

`4250 = 8500 * ((2)/(3))^r`

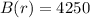
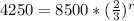
Divide both sides by 8500

`(4250)/(8500) = ((2)/(3))^r`

`(1)/(2) = ((2)/(3))^r`

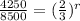
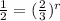
Take log of both sides

`log((1)/(2)) = log ((2)/(3))^r`

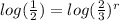
Apply law of logarithm

`log((1)/(2)) = r\ log ((2)/(3))`

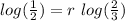
Make r the subject

`r = log((1)/(2)) / log ((2)/(3))`

`r = (-0.3010)/(-0.1761)`

`r = 1.71`

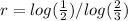
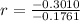
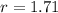
Hence, it reduces by 1/2 after every 1.71 seconds

Answer 2

Every second, the number of bacteria is multiplied by a factor of 0.67

Explanation:

Let's rewrite the base so that the exponent is just t.

(8/27)^t/3=((8/27)^1/3)t=(2/3)^t

Therefore, we can rewrite the modeling function as follows.

B(t)=8500⋅(2/3)t

According to this model, the number of bacteria is multiplied by 2/3 every second. Rounding this to two decimal places, we get 2/3 ≈0.67