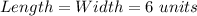Question

Chloe has enough sand to fill a sandbox with an extra area of 36 square units she wants the outer edge of the sandbox to use as little as Material possible

Answer 1

`Length = Width = 6\ units`

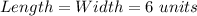
Explanation:

Given

`Area=36`

Required

The least possible material

Sandboxes usually, are rectangles or squares.

Using the above assumption, the area is calculated as:

`Area= Length * Width`

`Area= L* W`

`L * W = 36`

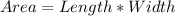
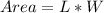
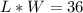
Make L the subject

`L = (36)/(W)`

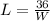
The material of the outer edge is calculated by the perimeter.

`Perimeter = 2 * (L +W)`

`P = 2 * (L + W)`

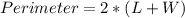
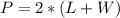
Substitute
`L = (36)/(W)`

`P = 2 * ((36)/(W) + W)`

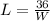
Open bracket

`P = (72)/(W) + 2W`

`P = 72W^(-1) +2W`

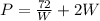
To get the minimum material needed, we differentiate P

`P' = -72W^(-2) + 2`

Set:
`P' = 0`

`-72W^(-2) + 2 = 0`

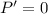
Collect like terms

`72W^(-2) = 2`

Divide both sides by 72

`W^(-2) = (2)/(72)`

`W^(-2) = (1)/(36)`

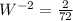
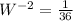
Rewrite as:

`(1)/(W^2) = (1)/(36)`

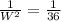
Take positive square roots of both sides

`(1)/(W) = (1)/(6)`

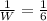
Cross multiply

`W = 6`

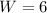
Recall that:
`L = (36)/(W)`

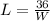
So, we have:

`L =(36)/(6)`

`L = 6`

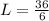
Hence, the dimension with the littlest material as possible is:

`Length = Width = 6\ units`