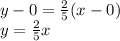Answer (assuming it can be in slope-intercept form):
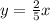
Explanation:
1) First, find the slope of the line using the slope formula,
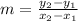 . Substitute the x and y values of (0,0) and (5,2) into the formula and simplify like so:
. Substitute the x and y values of (0,0) and (5,2) into the formula and simplify like so:
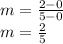
So, the slope is
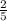 .
.
2) Now, use the point-slope formula to write the equation of the line. Using the point-slope formula
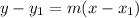 , substitute values for
, substitute values for
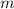 ,
,
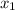 , and
, and
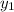 .
.
Since
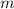 represents the slope, substitute
represents the slope, substitute
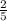 in its place. Since
in its place. Since
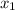 and
and
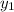 represent the x and y values of a point the line intersects, we can substitute the x and y values of one of the given points (I chose (0,0)) into the formula as well. Then, isolate y to put in slope-intercept form:
represent the x and y values of a point the line intersects, we can substitute the x and y values of one of the given points (I chose (0,0)) into the formula as well. Then, isolate y to put in slope-intercept form: