Answer:
Second answer
Explanation:
We are given
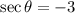 and
and
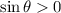 . What we have to find are
. What we have to find are
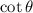 and
and
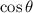 .
.
First, convert
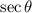 to
to
 via trigonometric identity. That gives us a new equation in form of
via trigonometric identity. That gives us a new equation in form of
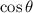 :
:
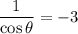
Multiply
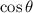 both sides to get rid of the denominator.
both sides to get rid of the denominator.
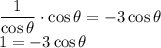
Then divide both sides by -3 to get
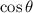 .
.
Hence,
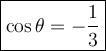
__________________________________________________________
Next, to find
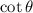 , convert it to
, convert it to
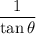 via trigonometric identity. Then we have to convert
via trigonometric identity. Then we have to convert
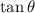 to
to
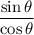 via another trigonometric identity. That gives us:
via another trigonometric identity. That gives us:
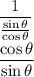
It seems that we do not know what
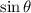 is but we can find it by using the identity
is but we can find it by using the identity
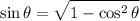 for
for
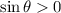 .
.
From
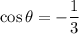 then
then
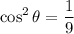 .
.
Therefore:
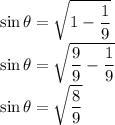
Then use the surd property to evaluate the square root.
Hence,
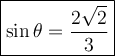
Now that we know what
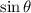 is. We can evaluate
is. We can evaluate
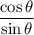 which is another form or identity of
which is another form or identity of
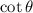 .
.
From the boxed values of
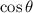 and
and
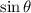 :-
:-

Then rationalize the value by multiplying both numerator and denominator with the denominator.
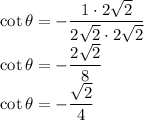
Hence,
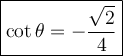
Therefore, the second choice is the answer.
__________________________________________________________
Summary
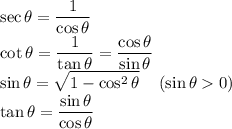
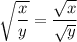
Let me know in the comment if you have any questions regarding this question or for clarification! Hope this helps as well.