Hello.
Let's solve the absolute value inequality.
In order to do that, let's imagine that |3x-4| is positive.
Since the absolute value of |3x-4| is 3x-4, we write 3x-4 and solve:

Now, move -4 to the right, using the opposite operation:
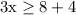
Add:
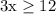
Divide both sides by 3:
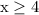
However, this is only 1 solution.
Let's imagine that |3x-4| is a negative number.
So, the inequality looks like so:
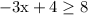
Move 4 to the right:

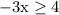
Divide both sides by -3:
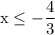
Therefore, the solutions are
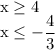
 Note:
Note:
If we divide both sides of an inequality by a negative number, we flip the inequality sign.
I hope this helps you.
Have a nice day.