Question

If y = 3x + 1 is changed to y = 4x + 1, how would the graph of the new function compare with

the first one?

Answer 1

The graph of the new function would be steeper than the first one.

Explanation:

Slope-intercept form

y= mx +c, where m is the gradient and c is the y-intercept. Note that in this form, the y term is the only term on the left-hand side of the equation and its coefficient is 1.

Identifying gradients

Since the two equations are in the slope-intercept form, we can easily identify their gradients from the coefficient of x.

The gradient of the first graph is 3, while that of the new function is 4.

Implications of a greater gradient

The gradient of a graph is how steep it is, or the change of y with respect to x. Also when we are given a linear graph without its equation, we can find its gradient using the formula:

`\boxed{ slope = (y _(1) - y_2 )/(x_1 - x_2) }`

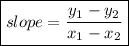
This formula can also be written as

`\boxed{ slope = (rise )/(run) }`

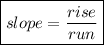
These formulas imply that the gradient is the looking at how much the y- coordinate changes with respect to x. The term 'gradient' and 'slope' have the same meaning and is used interchangeably here.

Given that the new function has a greater slope, it has a greater change in y with respect to x than the first graph. Thus, we see a steeper graph when y= 3x +1 is changed to y= 4x +1.

y- intercepts

The y-intercept does not change in this case and both graphs intercept the y-axis at y= 1.

Note

In the attached graph, the first graph is represented by the red line while the graph of the new function is in blue.