Answer:
The value of the test statistic is 2.8.
Explanation:
The test statistic is:

In which X is the sample mean,
 is the value expected value for the population mean,
is the value expected value for the population mean,
 is the standard deviation and n is the size of the sample.
is the standard deviation and n is the size of the sample.
Sales at a fast-food restaurant average $6,000 per day
This means that
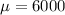
Sample of 49
This means that
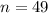
The sample showed average daily sales of $6,400.
This means that
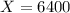
Population standard deviation is about $1,000.
This means that
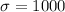
The value of the test statistic is


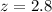
The value of the test statistic is 2.8.