Question

Need help with this question?

Answer 1

The equation is
`x^(2) +2\cdot x + 2 = 0`-

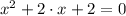Explanation:

According to the statement, we have a second order polynomial of the form
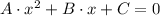`A\cdot x^(2)+ B\cdot x + C = 0`, whose solutions can be found by Quadratic Formula:

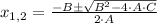`x_(1,2) = \frac{-B\pm \sqrt{B^(2)-4\cdot A\cdot C}}{2\cdot A}` (1)

Where
`A`,
`B` and
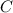`C` are the coefficients of the polynomial.

If roots are conjugated complex numbers, then:

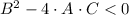`B^(2)-4\cdot A\cdot C < 0` (2)

`B^(2) < 4\cdot A \cdot C`

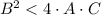
If we know that
`A = 1`,
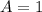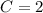`C = 2` and
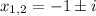`x_(1,2) = -1\pm i`, then we find that:

`-1\pm i = -(B)/(2)\pm \frac{\sqrt{B^(2)-8}}{2}`

`-2 \pm i\,2 = -B \pm \sqrt{B^(2)-8}`

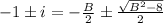
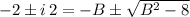
By comparing each side, we have the following system of equations:

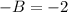`-B = -2` (3)

`\sqrt{B^(2)-8} = 2` (4)

Whose solution is
`B = 2`.

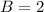In a nutshell, the equation is
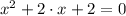`x^(2) +2\cdot x + 2 = 0`-