Question

Stephanie Robbins is attempting to perform an inventory analysis on one of her most popular products. Annual demand for this product is​ 5,000 units; carrying cost is​ $50 per unit per​ year; order costs for her company typically run nearly​ $30 per​ order; and lead time averages 10 days.​ (Assume 250 working days per​ year.) ​a) The economic order quantity is ​b) The average inventory is ​c) The optimal number of orders per year is ​d) The optimal number of working days between orders is ​e) The total annual inventory cost​ (carrying costordering ​cost) is ​ ​f) The reorder point is

Answer 1

Given :

The annual demand,
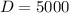`$D=5000$` units

Ordering cost,
`$S=\$30$`

Carrying cost,
`$H=\$50$`

Lead time, L = 10 days

Number of days per year = 250 days

So, average demand is d =
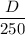`$(D)/(250)$` days

=
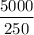`$(5000)/(250)$` = 20 units

a). The economic order quantity, Q =
`$\sqrt{(2DS)/(H)}$`

`$=\sqrt{(2* 5000 * 30)/(50)}$`

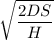
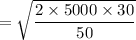
= 77 units

b). Average inventory =
`$(Q)/(2)$`

`$=(77)/(2)$`

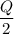
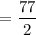
≈ 39 units

c). Number of orders per year =
`$(D)/(Q)$`

`$=(5000)/(77)$`

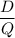
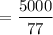
= 65 units

d). Time between orders =
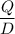`$(Q)/(D)$` x number of days per year

`$=(77)/(5000) *250$`

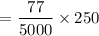
= 3.85

e). Annual ordering cost =
`$(D)/(Q) * S$`

`$=(5000)/(77) * 30$`

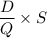
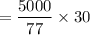
= $ 1948.05

Annual carrying cost =
`$(Q)/(2) * H$`

`$=(77)/(2) * 50$`

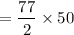
= $ 1925

Total annual cost of inventory = $ 1948.05 + $ 1925

= $ 3873.05

f). Reorder point =
`$d * L$`

`$=20 * 10$`

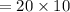
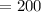`$=200$` units