Question

An engineer designed a valve that will regulate water pressure on an automobile engine. The engineer designed the valve such that it would produce a mean pressure of 4.6 pounds/square inch. It is believed that the valve performs above the specifications. The valve was tested on 26 engines and the mean pressure was 4.9 pounds/square inch with a variance of 0.81. A level of significance of 0.05 will be used. Assume the population distribution is approximately normal. Determine the decision rule for rejecting the null hypothesis. Round your answer to three decimal places.

Answer 1

Decision Rule; Reject H₀ if t > 1.708

Explanation:

Given the data in the question;

sample size n = 26

sample mean x' = 4.9

Variance = 0.81

standard deviation σ = √variance = √0.81 = 0.9

level of significance ∝ = 0.05

Claim;

Null hypothesis H₀ : μ = 4.6

Alternative hypothesis H₁ : μ > 4.6

Test Statistics;

Right tailed test

Now, decision rule for rejecting H₀;

degree of freedom df = n - 1 = 26 - 1 = 25

so, Right tailed test { > in H₁ }

Hence, Critical Value =
`t_{\alpha ,df` =
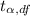`t_{0.05, 25` = 1.708

Decision Rule; Reject H₀ if t > 1.708