Answer:
The new velocity of the string is 100 centimeters per second (1 meter per second).
Step-by-step explanation:
The speed of a wave through a string (
 ), in meters per second, is defined by the following formula:
), in meters per second, is defined by the following formula:
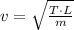 (1)
(1)
Where:
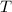 - Tension, in newtons.
- Tension, in newtons.
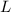 - Length of the string, in meters.
- Length of the string, in meters.
 - Mass of the string, in kilograms.
- Mass of the string, in kilograms.
The expression for initial and final speeds of the wave are:
Initial speed
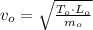 (2)
(2)
Final speed
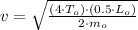
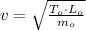 (3)
(3)
By (2), we conclude that:
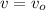
If we know that
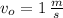 , then the new speed of the wave in the string is
, then the new speed of the wave in the string is
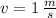 .
.