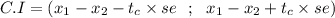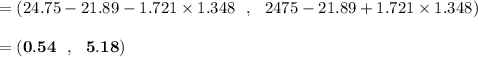Question

Data were collected on annual personal time (in hours) taken by a random sample of 16 women and 7 men employed by a medium sized company. The women took an average of 24.75 hours of personal time per year with a standard deviation of 2.84 hours. The men took an average of 21.89 hours of personal time per year with a standard deviation of 3.29 hours. The correct 90% confidence interval for the difference between women and men in the average number of hours of personal time taken per year is ________.

Answer 1

The correct 90% confidence interval for the difference between women and men in the average number of hours of personal time taken per year is

contained by the interval (0.54 , 5.18)

Explanation:

Given that:

for women

sample size = n₁ = 16

sample mean
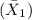`(\bar X_1)` = 24.75

standard deviation s₁ = 2.84

for men

sample size for men = n₂ = 7

sample mean
`(\bar X_2)` = 21.89

standard deviation s₂ = 3.29

degree of freedom =
`(n_1 + n_2 )-2`

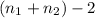
= 16 + 7 -2

= 21

The critical value for
`\alpha = 0.1 \ and \ df \ of \ 21 \ is :`

`t_(0.005;21)= 1.721`

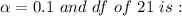
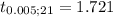
The pooled standard deviation can be calculated as follows since the population variances are assumed to be equivalent.

`s_p = \sqrt{((n_1 -1)s_1^2+(n_2-1)s_2^2)/(n_1+n_2-2)}`

`s_p = \sqrt{((16 -1)2.84^2+(7-1)3.29^2)/(16+7-2)}`

`s_p = \sqrt{((15)8.0656+(6)10.8241)/(21)}`

`s_p = 2.976`

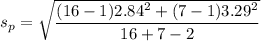
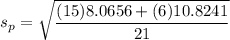
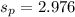
The standard error is estimated as follow:

`se = s_p\sqrt{(1)/(n_1) + (1)/(n_2)}`

`se = 2.976\sqrt{(1)/(16) + (1)/(7)}`

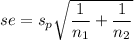
se = 1.348

Finally, the confidence interval
`C.I = ( x_1 -x_2 -t_c * se \ \ ; \ \ x_1-x_2 +t_c * se)`

`=(24.75 - 21.89 -1.721 * 1.348 \ \ , \ \ 2475 - 21.89 + 1.721 * 1.348) \\ \\ \mathbf{ = (0.54 \ \ , \ \ 5.18)}`