Question

Find the general solution of the differential equation and check the result by differentiation. (Use C for the constant of integration.)


`(dy)/(dx)` = 4x^1/6

Answer 1

For this we can first multiply both sides by dx:

`dy = 4x^(1/6)dx`

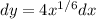
Next we can integrate both sides:

`\int dy = \int 4x^(1/6)dx\\`

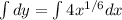
We can then solve both integrals to get:

`y = 4((6)/(7)x^{(7)/(6)}+C_1) = (24)/(7)x^{(7)/(6)}+C_2`

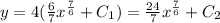
We can just say the constant is C2. So the answer is

`y = (24)/(7)x^{(7)/(6)}+C_2`

We can also check this by differentiating both sides. We will ultimately get the equation we with. If I made any mistakes or misread something, please let me know.