Answer:
(a)
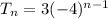
(b)

Explanation:
Given
The above sequence
Solving (a): The explicit formula
The given sequence is a geometric sequence because the common ratio (r) is:
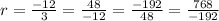

The explicit formula is calculated using the n term of an GP.
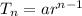
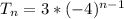
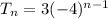
Solving (b): Summation notation.
This implies that the sum of the sequence.
To do this, we write Tn inside the summation sign
i.e.
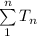
Substitute values for Tn
