Given:
The function is:
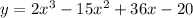
To find:
The turning points.
Solution:
We have,
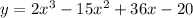
Differentiate the given function with respect to x.
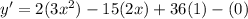
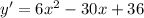
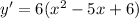
For turning point,
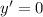 .
.
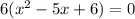
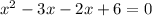
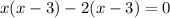
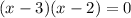
Using zero product property, we get
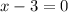 and
and
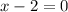
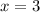 and
and
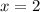
Therefore, the turning points of the given function are at
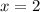 and
and
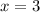 .
.