Question

A hexagon is inscribed in a circle As see in the picture.Find the length of an arc between consecutive vertices. Round to the nearest hundred

Need help homework

Answer 1

The length of the arc between consecutive vertices is:

`S=8.38\: in`

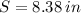
Explanation:

The angle between consecutive vertices is 60°, it is because it forms an equilateral triangle.

Now, the length arc is defined as:

`S=R\theta`

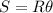
Where:

• R is the radius (R = 8 in)
• θ is the angle of the arc

We see the angle is in grades, but we need to convert it to radians.

`\theta=(60^(\circ))/(360^(\circ))(2\pi)`

`\theta=1.05\: rad`

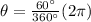
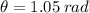
Finally, the length of the arc between consecutive vertices will be:

`S=8*1.05`

`S=8.38\: in`

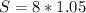
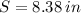
I hope it helps you!