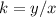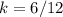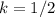Question

Which of the coordinate points below will fall on a line where the constant of proportionality is 1/4? Select all that apply. A) (4,1) B) (8,12) C) (12,3) D) (20,5) E) (12,6)

Answer 1

A) (4,1) C) (12,3) D) (20,5)

Explanation:

Required

Which has a constant of proportionality of 1/4

To solve this, we make use of:

`y = kx`

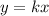
Where k is the constant of proportionality.

Solve for x

`k = y/x`

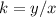
Testing the given options

A) (4,1)

`k = y/x`

`k =1/4`

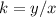
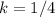
B) (8,12)

`k = y/x`

`k =12/8`

`k =3/2`

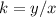
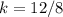
C) (12,3)

`k = y/x`

`k = 3/12`

`k = 1/4`

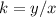
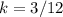
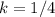
D) (20,5)

`k = y/x`

`k = 5/20`

`k = 1/4`

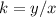
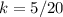
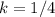
E) (12,6)

`k = y/x`

`k =6/12`

`k =1/2`