Question

A biologist studying trees constructed the confidence interval (0.14, 0.20) to estimate the proportion of trees in a large forest that are dead but still standing. Using the same confidence level, the interval was later revised because the sample proportion had been miscalculated. The correct sample proportion was 0.27. Which of the following statements about the revised interval based on the correct sample proportion is true?

A) The revised interval is narrower than the original interval because the correct sample proportion is farther from 0.5 than the calculated proportion is
B) The revised interval is narrower than the original interval because the correct sample proportion is closer to 0.5 than the mis-calculated proportion is
C) The revised interval is wider than the original interval because the correct sample proportion is farther from 0.5 than the mis-calculated proportion is
D) The revised interval is wider than the original interval because the corect sample proportion is closer to 0.5 than the mis-calculated proportion is.
E) The revised interval has the same width as the original interval.

Answer 1

D) The revised interval is wider than the original interval because the corect sample proportion is closer to 0.5 than the mis-calculated proportion is.

Explanation:

In a sample with a number n of people surveyed with a probability of a success of
`\pi`, and a confidence level of
`1-\alpha`, we have the following confidence interval of proportions.

`\pi \pm z\sqrt{(\pi(1-\pi))/(n)}`

In which

z is the zscore that has a pvalue of
`1 - (\alpha)/(2)`.

The margin of error is:

`M = z\sqrt{(\pi(1-\pi))/(n)}`

The larger the closer to 0.5 the value of
`\pi`, the larger the margin of error and the wider the interval is.

A biologist studying trees constructed the confidence interval (0.14, 0.20)

This means that the estimate used was of:

`\pi = (0.14 + 0.2)/(2) = (0.34)/(2) = 0.17`

The correct sample proportion was 0.27.

With
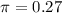`\pi = 0.27`, the margin of error is larger as 0.27 is closer to 0.5 than 0.17. Thus, the revised interval will be wider, and the correct answer is given by option D.