Question

h(x) = x ^ 2 - 7x - 8 1) What are the zeros of the function? Write the smaller first, and the larger second smaller I largerx = 2 ) What is the vertex of the parabola ?

Answer 1

The zeros are x = -1 and x = 8

The vertex is (3.5, -20.25)

Explanation:

When we have a quadratic equation like:

y = a*x^2 + b*x + c

The zeros of the function are the values of x such that:

a*x^2 + b*x + c = 0

And the solutions are given by the Bhaskara's equation, which is:

`x = (-b \pm √(b^2 - 4*a*c) )/(2*a)`

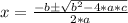
And the vertex is at:

x = -b/2a

The y-value at the vertex is the function evaluated in that point.

In this case, we have the equation:

h(x) = x^2 - 7*x - 8

Then:

a = 1

b = -7

c= -8

Replacing these in the Bhaskara's equation we get:

`x = (-(-7) \pm √((-7)^2-4*1*(-8)) )/(2*1) = (7 \pm 9 )/(2)`

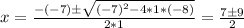
Then the two solutions are:

x = (7 - 9)/2 = -2/2 = -1 (this is the smaller one)

and

x = (7 + 9)/2 = 16/2 = 8 (this is the larger one)

And we will have the vertex at:

x = -(-7)/2*1 = 7/2 = 3.5

Evaluating h(x) in 3.5 we get:

h(3.5) = (3.5)^2 - 7*(3.5) - 8 = -20.25

Then the vertex is the point:

(3.5, -20.25)