Question

Simplify the expression: (in the image attached)

Answer 1

`(y(y+2x^2))/(x(5y^2-6x)`

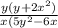
Explanation:

Lets do the numerator and denominator seperately:

Numerator:

1/x^2 + 2/y

Find common denominator and add these 2 fractions:

This is x^2y (I just multiplied the 2 denominators together’

Now, do what you have done to x^2 to make it x^2y, ie. multiplied by y, to the 1. This = y

And do what you have done to y to make it x^2y, ie. multiplied by x^2, to the 2. This =
`2^(2)`

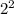
Now, arrange all numbers we have found into the correct order in the fraction. This is:

`(y+2x^(2))/(x^(2) y)`

Denominator:

5/x - 6/y^2

Find the common denominator and subtract these two fractions:

This is xy^2

Now, do what you have done to x to make it xy^2, ie. multiply by y^2, to the 5. This = 5y^2

And do what you have done to the y^2 to make it xy^2, ie. multiply by x, to the 6, this is = 6x

Now, arrange all the numbers we have found into the correct order in the fraction

`(5y^(2)-6x)/(xy^2)`

Now that we have the numerator and the denominator, we can solve the equation.

The original question asks us to divide the 2 fractions, so:

`(y+2x^(2))/(x^(2) y)` divided by
`(5y^(2)-6x)/(xy^2)`

For the division of fractions, you just have to multiply the inverse of the 2nd fraction by the first, so

`(y+2x^(2))/(x^(2) y)` x
`(xy^2)/(5y^2-6x)`

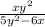
Use cross multiplication to simplify the above expression to:

`(y(y+2x^2))/(x(5y^2-6x)`

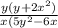
Hope this helps, sorry its long ...

Answer 2

Explanation:

Hey there!

`\tt{((1)/(x^2) + (2)/(y))/((5)/(x) - (6)/(y^2))}`

So, what we can do here is first take the Least Common Multiple here, on both Numerator and Denominator.

`\tt{((y + 2y^2 (1))/(x^2 y (2)))/((5y^2 - 6x (3) )/(xy^2 (4)))}`

[The number in brackets is for the next step :-

When we will further simplify it, we will multiply 1st with 4th and 2nd with 3rd.

`\tt{(y + 2y^2 * xy^2 )/(x^2 y * 5y^2 - 6x )}`

`\tt{(y + 2y^2 * y )/(x * 5y^2 - 6x )}` is the framed answer.