Given:
A figure of a circle and inscribed quadrilateral JKLM.
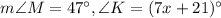
To find:
The value of x.
Solution:
The inscribed quadrilateral JKLM in the circle I is a cyclic quadrilateral and the opposite angles of a cyclic quadrilateral are supplementary angles.
Angle M and angle K are opposite angles of a cyclic quadrilateral, it means they are supplementary angles and their sum is 180 degrees.
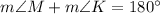
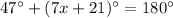
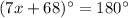
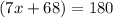
Isolate the variable x.
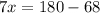
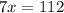
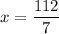
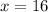
Therefore, the value of x is 16.