Question

Two similar solids have a scale factor or 6:7.

What is ratio of their volumes, expressed in lowest terms?

Answer 1

Ratio's is 216 : 343

Step-by-step explanation:

Volume of one solid is x, and the other is y

Scale factor = 6 : 7

Volume of solid = a³

Solve:

`(x)/(y)=((6)/(7))^(3)`

`(x)/(y)=(216)/(343)`

Hence, the volume of one solid is 216 and the other is 343

As a Ratio:

216 : 343

Answer 2

ratio's of their volume is 216 : 343

Step-by-step explanation:

Let volume of one solid be x, another be y

given scale factor = 6 : 7

volume of solid = a³

solve:

`\sf (x)/(y) = ((6)/(7) )^3}`

`\sf (x)/(y) = (216)/(343) }`

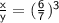
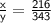
║ Therefore volume of one solid is 216 and another 343 ║

In ratio form:

216 : 343