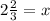Answer:
y =
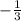
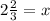
Explanation:
To solve a system of equations, solve one or both of the equations for the same variable. Then multiply one of the equations such that the coefficients of one variable are the additive inverse of the variable in the other equation. After doing so, add the two equations, then solve for the other variable using inverse operations. Finally, substitute the value of the other variable into one of the original equations in the system and solve for the unknown variable.
2x + y = 3
y = x - 2
First, manipulate the first equation such that the equation is solved for (y), this can be done using inverse operations,
y = 3 - 2x
y = x - 2
Now multiply the second equation by (2) so that the (x) coefficients are additive inverses of each other,
y = 3 - 2x
2y = 2x - 4
Add the equations,
3y = -1
Inverse operations,
3y = -1
/3 /3
y =
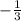
Now back solve, substitute the value of (y) into the equation and solve for (x),
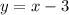
Substitute,
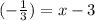
+3