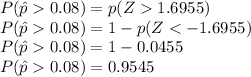Question

A scientist claims that 6% of viruses are airborne. (a) If the scientist is accurate, what is the probability that the proportion of airborne viruses in a sample of 529 viruses would be greater than 8%? Round your answer to four decimal places.

Answer 1

Probability that the proportion of airborne viruses in a sample of 529 viruses would be greater than 8% is 0.9545.

Step-by-step explanation:

For the given population the distribution of air-borne viruses is given as 6%. Now for this the value of Z score is given as

`Z=\frac{\hat{p}-p}{\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}}`

Here

• 
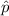  `\hat{p}` is the sample measure which is 8% or 0.08
• p is the population measure which is 6% or 0.06
• n is the number of samples which is 529

So the Z score is given as

`Z=\frac{\hat{p}-p}{\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}}\\Z=\frac{0.08-0.06}{\sqrt{(0.08(1-0.08))/(529)}}\\Z=\frac{0.02}{\sqrt{(0.08(0.92))/(529)}}\\Z=\frac{0.02}{\sqrt{(0.0736)/(529)}}\\Z=(0.02)/(0.01179)\\Z=1.6955`

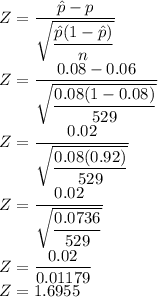
For this the score, the value of probability is calculated from the table as below:

`P(\hat{p}>0.08)=p(Z>1.6955)\\=1-p(Z<-1.6955)`

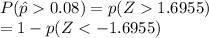
Here value of p(Z<-1.6955) is given as 0.0455

`P(\hat{p}>0.08)=p(Z>1.6955)\\P(\hat{p}>0.08)=1-p(Z<-1.6955)\\P(\hat{p}>0.08)=1-0.0455\\P(\hat{p}>0.08)=0.9545`