Question

What is the perimeter of the rectangle whose vertices are at (6, 3), (−6, 3), (−6, −1), and (6, −1)?

Answer 1

Given:

The vertices of a rectangle are (6, 3), (−6, 3), (−6, −1), and (6, −1).

To find:

The perimeter of the rectangle.

Solution:

Distance formula:

`d=√((x_2-x_1)^2-(y_2-y_1)^2)`

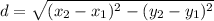
Let the vertices of a rectangle are A(6, 3), B(−6, 3), C(−6, −1), and D(6, −1).

Using the distance formula, we get

`AB=√((-6-6)^2-(3-3)^2)`

`AB=√((-12)^2-(0)^2)`

`AB=√(144)`

`AB=12`

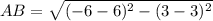
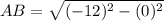
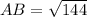
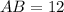
Similarly,

`BC=√(\left(-6-\left(-6\right)\right)^2+\left(-1-3\right)^2)=4`

`CD=√(\left(6-\left(-6\right)\right)^2+\left(-1-\left(-1\right)\right)^2)=12`

`AD√(\left(6-6\right)^2+\left(-1-3\right)^2)=4`

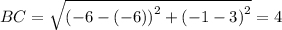
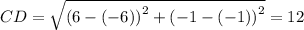
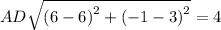
Now, the perimeter of the rectangle is:

`Perimeter=AB+BC+CD+AD`

`Perimeter=12+4+12+4`

`Perimeter=32`

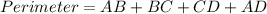
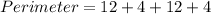
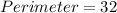
Therefore, the perimeter of the rectangle is 32 units.