Question

The function D(t) defines a traveler's distance from home, in miles, as a function of time, in hours.

Answer 1

Question:

The function D(t) defines a traveler’s distance from home, in miles, as a function of time, in hours.

`D(t) = \left \{ {{300t + 125,\ 0 \le t < 2.5} \atop {880,\ 2.5 \le t \le 3.5}} \right.`

`75t + 612.5,\ 3.5 < t \le 6`

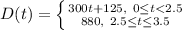
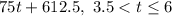
Which times and distances are represented by the function?

(a)The starting distance, at 0 hours, is 300 miles.

(b) At 2 hours, the traveler is 725 miles from home.

(c) At 2.5 hours, the traveler is 875 miles from home.

(d) At 3 hours, the distance is constant, at 880 miles.

(e) The total distance from home after 6 hours is 1,062.5 miles.

Answer:

• At 2 hours, the traveler is 725 miles from home.
• At 3 hours, the distance is constant, at 880 miles.
• The total distance from home after 6 hours is 1,062.5 miles.

Explanation:

Given

`D(t) = \left \{ {{300t + 125,\ 0 \le t < 2.5} \atop {880,\ 2.5 \le t \le 3.5}} \right.`

`75t + 612.5,\ 3.5 < t \le 6`

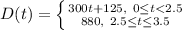
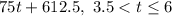
Required

Select the right options

(a) t = 0 hours, d(t) = 300 miles.

To check this, we make use of:

`D(t) = 300t + 125, 0 \le t < 2.5`

So, we have:

`D(0) = 300*0 + 125`

`D(0) = 0+125`

`D(0) = 125`

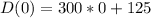
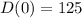
(a) is incorrect

(b) t =2 hours, d(t) = 725 miles

To check this, we make use of:

`D(t) = 300t + 125, 0 \le t < 2.5`

`D(2) = 300 *2 + 125`

`D(2) = 600 + 125`

`D(2) = 725`

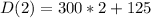
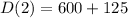
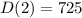
(b) is correct

(c) t = 2.5 hours, d(t) = 875 miles

To check this, we make use of:

`D(t) = 800, 2.5 \le t \le 3.5`

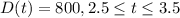
So, we have:

`D(2.5) = 800`

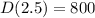
(c) is incorrect

(d) t = 3 hours, d(t) = 880 miles constant

To check this, we make use of:

`D(t) = 800, 2.5 \le t \le 3.5`

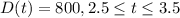
So, we have:

`D(3) = 800`

(d) is correct

(e) t = 6 hours d = 1,062.5 miles.

To check this, we make use of:

`D(t) =75t + 612.5,\ 3.5 < t \le 6`

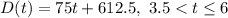
So, we have:

`D(6) =75*6 + 612.5`

`D(6) =450 + 612.5`

`D(6) =1062.5`

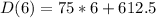
(e) is correct