Question

Which is an example of a quadratic function whose graph opens downward and has its vertex at (0, 1)?

A. y = −x^2 + 1
B. y = x^2 + x − 1
C. y = x^2 + 4x + 1
D. y = x^2 − 1

Answer 1

Given:

The graph of a quadratic function opens downward and has its vertex at (0, 1).

To find:

The quadratic function.

Solution:

The vertex form of a quadratic function is:

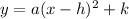`y=a(x-h)^2+k` ...(i)

Where, a is a constant and (h,k) is the vertex.

If a<0, then graph opens downward and if a>0, then graph opens upward.

It is given that the quadratic function opens downward and has its vertex at (0, 1). It means a must be negative.

Putting h=0 and k=1 in (i), we get

`y=a(x-0)^2+1`

`y=ax^2+1`

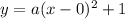
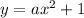
For
`a=-1`,

`y=(-1)x^2+1`

`y=x^2+1`

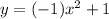
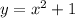
So, option A is correct.

In other options the leading coefficient is positive it means their graphs open upward. So, options B, C and D are incorrect.

Therefore, the correct option is A.