Question

A coffee shop buys 2000 bags of their most popular coffee beans each month. The cost of ordering and receiving shipments is $12 per order. Accounting estimates annual carrying costs are $3.60. The supplier lead time is 8 operating days. The shop operates 240 days per year. Each order is received from the supplier in a single delivery. There are no quantity discounts.

Required:
a. What quantity should the shop order with each order?
b. How many times per year will the shop order?
c. How many operating days will elapse between two consecutive orders?
d. What is the reorder point if the company wishes to carry a safety stock of 10 bags?
e. What is the store's minimum total annual cost of placing orders & carrying inventory?

Answer 1

The optimal order quantity, EOQ =
`$\sqrt{\frac{2 * \text{demand}* \text{ordering cost}}{\text{holding cost}}}$`

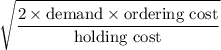
EOQ =
`$\sqrt{(2 * 2000 * 12)/(3.6)}$`

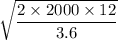
= 115.47

The expected number of orders =
`$\frac{\text{demand}}{EOQ}$`

`$=(2000)/(115.47)$`

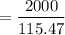
= 17.32

The daily demand = demand / number of working days

`$=(2000)/(240)$`

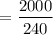
= 8.33

The time between the orders = EOQ / daily demand

`$=(115.47)/(8.33)$`

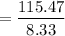
= 13.86 days

ROP = ( Daily demand x lead time ) + safety stock

`$=(8.33 * 8)+10$`

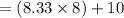
= 76.64

The annual holding cost =
`$(EOQ)/(2) * \text{holding cost}$`

`$=(115.47)/(2) * 3.6$`

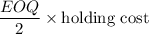
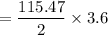
= 207.85

The annual ordering cost =
`$\frac{\text{demand}}{EOQ} * \text{ordering cost}$`

`$=(2000)/(115.47) * 12$`

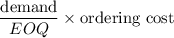
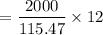
= 207.85

So the total inventory cost = annual holding cost + annual ordering cost

= 207.85 + 207.85

= 415.7