Given:
The height of 44 students (in centimeter) are presented in the given frequency distribution.
To find:
The median of the given data.
Solution:
The given intervals are inclusive first make the intervals exclusive by adding 0.5 in upper limit and by subtracting 0.5 from the lower limit.
The complete frequency distribution table is shown below:
Height Frequency L <cf
182 - 188 1 181.5 - 188.5 44
175 - 181 3 174.5 - 181.5 43
168 - 174 6 167.5 - 174.5 40
161 - 167 15 160.5 - 167.5 34 Median class
154 - 160 12 153.5 - 160.5 19
147 - 153 4 146.5 - 153.5 7
140 - 146 3 139.5 - 146.5 3
We have,
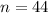 .
.
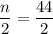
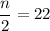
The 22th term is include in the class 160.5 - 167.5 because is cf is greater than 22 but the cf of o preceding class is less than 22. So, it is the median class is 160.5 - 167.5.
Formula for median:
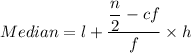
Where, l is the lower limit of median class, cf is the cumulative frequency of preceding class, f is the frequency of median class and h is the size of the class.
Now,
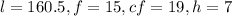 .
.
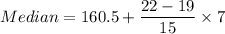
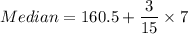
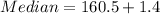
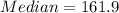
Therefore, the median of the given data table is 161.9.