Explanation:
We have cartisean points. We are trying to find polar points.
We can find r by applying the pythagorean theorem to the x value and y values.
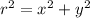
And to find theta, notice how a right triangle is created if we draw the base(the x value) and the height(y value). We also just found our r( hypotenuse) so ignore that. We know the opposite side and the adjacent side originally. so we can use the tangent function.
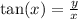
Remeber since we are trying to find the angle measure, use inverse tan function
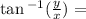
Answers For 2,5
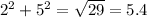
So r=sqr root of 29
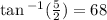
So the answer is (sqr root of 29,68).
For -3,3
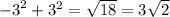
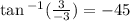
Use the identity
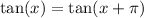
So that means
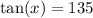
So our points are
(3 times sqr root of 2, 135)
For 5,-3.5
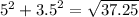
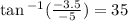
So our points are (sqr root of 37.25, 35)
For (0,-5.4)
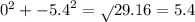
So r=5.4
![\tan {}^( - 1) (0) = undefined]()
So our points are (5.4, undefined)