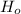Answer:
Explanation:
The table can be computed as:
Advertising Expenses ($ million) Number of companies
25 up to 35 4
35 up to 45 19
45 up to 55 27
55 up to 65 16
65 up to 75 9
TOTAL 75
Let's find the probabilities first:
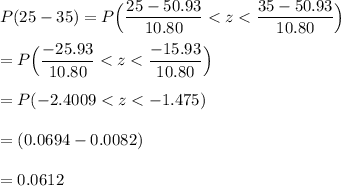
For 35 up to 45
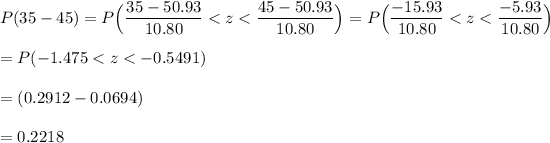
For 45 up to 55
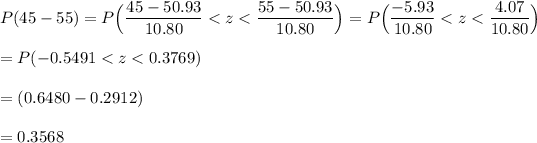
For 55 up to 65

For 65 up to 75

Chi-Square Table can be computed as follows:
Expense No of Probabilities(P) Expe
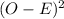
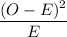
compa cted E (n*p)
nies (O)
25-35 4 0.0612 75*0.0612 = 4.59 0.3481 0.0758
35-45 19 0.2218 75*0.2218 = 16.635 5.5932 0.3362
45-55 27 0.3568 75*0.3568 = 26.76 0.0576 0.021
55-65 16 0.2552 75*0.2552 = 19.14 9.8596 0.5151
65-75 9 0.0839 75*0.0839 = 6.2925 7.331 1.1650
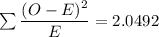
Using the Chi-square formula:
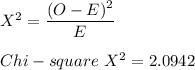
Null hypothesis:
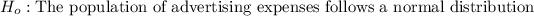
Alternative hypothesis:
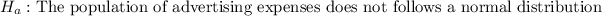
Assume that:
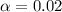
degree of freedom:
= n-1
= 5 -1
= 4
Critical value from
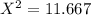
Decision rule: To reject
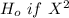 test statistics is greater than
test statistics is greater than
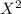 tabulated.
tabulated.
Conclusion: Since
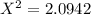 is less than critical value 11.667. Then we fail to reject
is less than critical value 11.667. Then we fail to reject