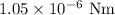Answer:
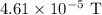
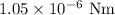
Step-by-step explanation:
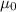 = Vacuum permeability =
= Vacuum permeability =
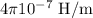
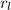 = Radius of loop = 15 cm
= Radius of loop = 15 cm
 = Current in loop = 11 A
= Current in loop = 11 A
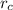 = Radius of coil = 0.76 cm
= Radius of coil = 0.76 cm
N = Number of turns of coil = 66
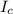 = Current in coil = 1.9 A
= Current in coil = 1.9 A
Magnetic field is given by
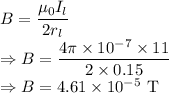
Magnitude of magnetic field produced by the loop at its center is
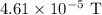 .
.
Torque is given by
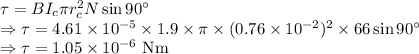
Magnitude of torque on the coil due to the loop is