Question

Instructions: Please make sure that you show all your work when solving the problems. Feel free to make any assumptions whenever you feel necessary. Just make sure that you clearly state your assumptions.

Analysts expect MC, Co. to maintain a dividend payout ratio of 35% and enjoy an expected growth rate of 12% per year for the next 5 years. After the fifth year, all earnings will be paid out as dividends. The required rate of return on MC, Co equity is 8%.
a. Given that the last dividend paid was $0.5 and the current market price of the stock is $15, what growth rate does the market expect for MC, Co?
b. At what price would the analysts value the stock under their own expectations?
c. Suppose 5 years have gone by and the company has to make a decision on how to move forward. It can either pay out all earnings as dividends without considering any growth opportunities, or choose a growth strategy where the company will expand into new lines of business in global markets. If the management chooses this strategy, the payout ratio will be reduced down to 20% from 35%, and the company will be able to maintain a growth rate of 7% forever. Which strategy should the management choose to maximize shareholder value?

Answer 1

Step-by-step explanation:

From the given information:

The current price =
`\frac{Dividend(D_o) * (1+ Growth \ rate) }{\text{Cost of capital -Growth rate}}`

`15 = (0.50 * (1+ Growth rate))/(8\%-Growth rate)`

`15 * (8 -Growth \ rate) = 0.50 +(0.50 * growth \ rate)`

`1.20 - (15 * Growth \ rate) = 0.50 + (0.50 * growth \ rate)`

`0.70 = (15 * growth \ rate) \\ \\ Growth \ rate = (0.70)/(15.50) \\ \\ Growth \ rate = 0.04516 \\ \\ Growth \ rate \simeq 4.52\% \\ \\`

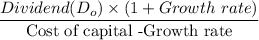
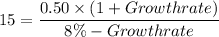
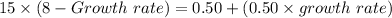
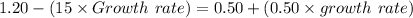
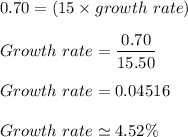
2. The value of the stock

Calculate the earnings at the end of 5 years:

`Earnings (E_o) * Dividend \ payout \ ratio = Dividend (D_o) \\ \\ Earnings (E_o) * 35\% = \$0.50 \\ \\ Earnings (E_o) =(\$0.50)/(35\%) \\ \\ = \$1.42857`

`Earnings (E_5) year \ 5 = Earnings (E_o) * (1 + Growth \ rate)^(no \ of \ years) \\ \\ Earnings (E_5) year \ 5 = \$1.42857 * (1 + 12\%)^5 \\ \\ Earnings (E_5) year \ 5 = \$2.51763`

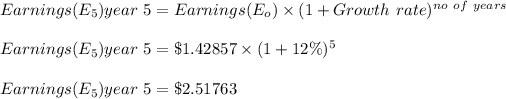
Terminal value year 5 =
`(Earnings (E_5) * (1+ Growth \ rate))/(Interest \ rate - Growth \ rate)`

`=(\$2.51763* (1+0.04516))/(8\%-0.04516)`

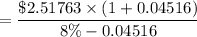
=$75.526

Discount all potential future cash flows as follows to determine the stock's value:

`\text{Value of stock today} =\bigg( \sum \limits ^{\text{no of years}}_(year =1) \frac{Dividend (D_o) * 1 +Growth rate ) ^{\text{no of years}}}{(1+ interest rate )^(no\ of\ years) }`

`+ (Terminal\ Value )/((1+interest \ rate )^(no \ of \ years)) \Bigg)`

`\implies \bigg((\$0.50* (1 + 12\%)^1) )/((1+ 8\%)^(1) )+ (\$0.50* (1+12\%)^2 )/((1+8\% )^(2))+ (\$0.50* (1+12\%)^3 )/((1+8\% )^(3)) + (\$0.50* (1+12\%)^4 )/((1+8\% )^(4)) + (\$0.50* (1+12\%)^5 )/((1+8\% )^(5)) + (\$75.526)/((1+8\% )^(5)) \bigg )`

`\implies \bigg((\$0.5600)/(1.0800)+(\$0.62720)/(1.16640)+(\$0.70246)/(1.2597)+(\$0.78676)/(1.3605)+(\$0.88117)/(1.4693)+ (\$75.526)/(1.4693) \bigg)`

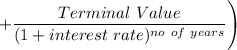
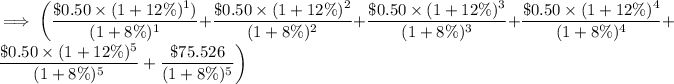
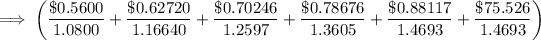
=$ 54.1945

As a result, the analysts value the stock at $54.20, which is below their own estimates.

3. The value of the stock

Calculate the earnings at the end of 5 years:

`Earnings (E_o) * Dividend payout ratio = Dividend (D_o) \\ \\ Earnings (E_o) * 35\% = \$0.50 \\ \\ Earnings (E_o) =(\$0.50)/(35\%)\\ \\ = \$1.42857`

`Earnings (E_5) year \ 5 = Earnings (E_o) * (1 + Growth \ rate)^(no \ of \ years) \\ \\ Earnings (E_5) year \ 5 = \$1.42857 * (1 + 12\%)^5 \\ \\ Earnings (E_5) year \ 5 = \$2.51763 \\ \\`

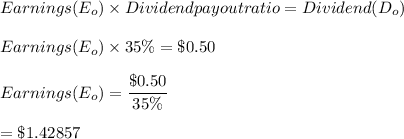
Terminal value year 5 =
`(Earnings (E_5) * (1+ Growth \ rate)* dividend \ payout \ ratio)/(Interest \ rate - Growth \ rate)`

`=(\$2.51763* (1+ 7 \%) * 20\%)/(8\%-7\%)`

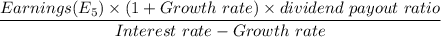
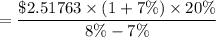
=$53.8773

Discount all potential cash flows as follows to determine the stock's value:

`\text{Value of stock today} =\bigg( \sum \limits ^{\text{no of years}}_(year =1) \frac{Dividend (D_o) * 1 + Growth rate ) ^{\text{no of years}}}{(1+ interest rate )^(no \ of\ years) }+ (Terminal \ Value )/((1+interest \ rate )^(no \ of \ years )) \bigg)`

`\implies \bigg( (\$0.50* (1 + 12\%)^1) )/((1+ 8\%)^(1) )+ (\$0.50* (1+12\%)^2 )/((1+8\% )^(2))+ (\$0.50* (1+12\%)^3 )/((1+8\% )^(3)) + (\$0.50* (1+12\%)^4 )/((1+8\% )^(4)) + (\$0.50* (1+12\%)^5 )/((1+8\% )^(5)) + (\$53.8773)/((1+8\% )^(5)) \bigg)`

`\implies \bigg ((\$0.5600)/(1.0800)+(\$0.62720)/(1.16640)+(\$0.70246)/(1.2597)+(\$0.78676)/(1.3605)+(\$0.88117)/(1.4693)+ (\$53.8773)/(1.4693) \bigg)`

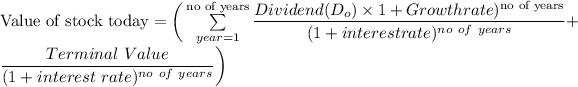
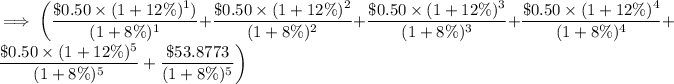
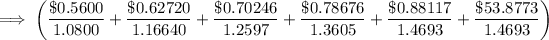
=$39.460

As a result, the price is $39.460, and the other strategy would raise the value of the shareholders. Not this one, since paying a 100% dividend would result in a price of $54.20, which is higher than the current price.

Notice that the third question depicts the situation after 5 years, but the final decision will be the same since we are discounting in current terms. If compounding is used, the future value over 5 years is just the same as the first choice, which is the better option.

The presumption in the second portion is that after 5 years, the steady growth rate would be the same as measured in the first part (1).