Question

A 20-question multiple choice quiz has five choices for each question. Suppose that a student just guesses, hoping to get a high score. The teacher carries out a hypothesis test to determine whether the student was just guessing. The null hypothesis is p = 0.20, where p is the probability of a correct answer.

a. Which of the following describes the value of the z-test statistic that is likely to result? Explain your choice.

i. The z-test statistic will be close to 0.
ii. the z-test statistic will be far from 0.

b. Which of the following describes the p-value that is likely to result? Explain your choice.

i. The p-value will be small.
ii. The p-value will not be small.

Answer 1

a) i. The z-test statistic will be close to 0, as the sample mean and the tested proportion are expected to be close values.

b) ii. The p-value will not be small, as the z-statistic is close to 0.

Explanation:

The null hypothesis is p = 0.20

The teacher carries out a hypothesis test to determine whether the student was just guessing.

Test if the proportion is different from 0.2. So the alternate hypothesis is:

`H_(a): p \\eq 0.2`

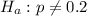
Five choices for each question, one of which is correct.

Probability of having a correct answer is
`X = (1)/(5) = 0.2`

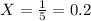
The test statistic is:

`z = (X - \mu)/((\sigma)/(√(n)))`

In which X is the sample mean,
`\mu` is the value tested at the null hypothesis,
`\sigma` is the standard deviation and n is the size of the sample.

a. Which of the following describes the value of the z-test statistic that is likely to result?

In this question,
`X = p = \mu`, which meas that the numerator of the z-statistic will be close to 0, which means that the z-test statistic will be close to 0.

b. Which of the following describes the p-value that is likely to result?

pvalue is 2 multiplied by the pvalue of Z(if negative), or 1 subtracted by the pvalue of Z(if positive).

Since the value of Z is close to 0, either the pvalue of Z or 1 subtracted by the pvalue of Z is close to 0.5, and multiplied by 2 will be close to 1. So, as Z is close to 0, the pvalue will not be small.