Answer:
The turntable's angular speed after the event is 28.687 revolutions per minute.
Step-by-step explanation:
The system formed by the turntable and the two block are not under the effect of any external force, so we can apply the Principle of Conservation of Angular Momentum, which states that:
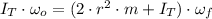 (1)
(1)
Where:
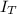 - Moment of inertia of the turntable, in kilogram-square meters.
- Moment of inertia of the turntable, in kilogram-square meters.
 - Distance of the block regarding the center of the turntable, in meters.
- Distance of the block regarding the center of the turntable, in meters.
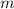 - Mass of the object, in kilograms.
- Mass of the object, in kilograms.
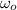 - Initial angular speed of the turntable, in radians per second.
- Initial angular speed of the turntable, in radians per second.
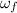 - Final angular speed of the turntable-objects system, in radians per second.
- Final angular speed of the turntable-objects system, in radians per second.
In addition, the momentum of inertia of the turntable is determined by following formula:
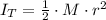 (2)
(2)
Where
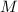 is the mass of the turntable, in kilograms.
is the mass of the turntable, in kilograms.
If we know that
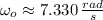 ,
,
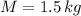 ,
,
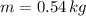 and
and
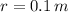 , then the angular speed of the turntable after the event is:
, then the angular speed of the turntable after the event is:
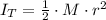
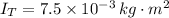
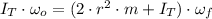
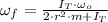
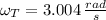 (
(
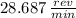 )
)
The turntable's angular speed after the event is 28.687 revolutions per minute.