Answer:
Area of the shaded region = 450.52 square inch
Explanation:
Area of the shaded region = Area of the circle - Area of the right triangle inscribed in the semicircle
By applying Pythagoras theorem in the given right triangle,
(Hypotenuse)² = (leg 1)² + (leg 2)²
= (21)² + (20)²
Hypotenuse =
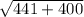
=

= 29
Since, hypotenuse of the right triangle is the diameter of the circle.
Therefore, radius of the circle =
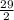
= 14.5 in.
Area of the circle = πr²
= π(14.5)²
= 660.519
≈ 660.52 in²
Area of the right triangle =
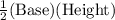
=

= 210 in²
Area of the shaded region = 660.52 - 210
= 450.52 square inch