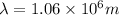Question

An electromagnetic wave with frequency 65.0Hz travels in an insulating magnetic material that has dielectric constant 3.64 and relative permeability 5.18 at this frequency. The electric field has amplitude 7.20×10−3V/m. What is the wavelength of the wave?

Answer 1

The wavelength of the wave is
`1.06*10^6 m`

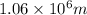
Step-by-step explanation:

Lets calculate

We know an electromagnetic wave is propagating through an insulating magnetic material of dielectric constant K and relative permeability
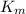`K_m` ,then the speed of the wave in this dielectric medium is
`\\u` is less than the speed of the light c and is given by a relation

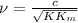`\\u=(c)/(√(KK_m) )` --------- 1

In case the electromagnetic wave propagating through the insulating magnetic material , the amplitudes of electric and magnetic fields are related as -

`E_m_a_x= \\u B_m_a_x`

The magnitude of the 'time averaged value' of the pointing vector is called the intensity of the wave and is given by a relation

`I = S_a_v`

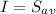
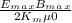`(E_m_a_xB_m_a_x)/(2K_m\mu0)`----------- 3

now , we will find the speed of the propagation of an electromagnetic wave by using equation 1

`\\u=(c)/(√(KK_m) )`

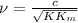
Putting the values ,

=
`\\u= (3.00*10^8)/(√((3.64)(5.18)) )`

=
`0.6908*10^8m/s`

=
`6.91*10^7m/s`

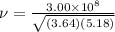
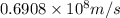
Now , using this above solution , we will find the wavelength of the wave -

`\lambda=(\\u)/(f)`

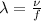
Putting the values from above equations -

`(6.91*10^7m/s)/(65.0Hz)`

`\lambda= 1.06*10^6 m`

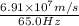
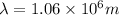
Hence , the answer is
`\lambda= 1.06*10^6 m`