Question

LAN tosses a bone up In the air for his dog, Spot. The height, h, in feet, that Spot is above the ground at the time t seconds after she jumps for the bone can be represented by the function h(t) = -16t^2 + 20t. What is Spots average rate of ascent, in feet per second, from the time she jumps into the air to the Time she catches the bone at t = 1/2 second?

Answer 1

The rate of change is 12ft/s

Explanation:

Given

`h(t) = -16t^2 + 20t`

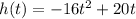
Required

Rate of change from when she jumps till 1/2s

The time she jumps is represented as: t = 0

So, calculate h(0)

`h(t) = -16t^2 + 20t`

`h(0) = -16 * 0^2 + 20 * 0 = 0`

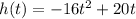
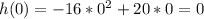
At t = 1/2

`h(t) = -16t^2 + 20t`

`h(1/2) = -16 * 1/2^2 + 20 * 1/2 = 6`

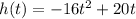
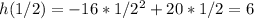
Rate of change is calculated as:

`Rate = (f(b) - f(a))/(b - a)`

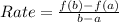
In this case:

`Rate = (h(b) - h(a))/(b - a)`

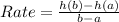
Where

`(a,b) = (0,1/2)`

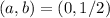
So, we have:

`Rate = (h(b) - h(a))/(b - a)`

`Rate = (h(1/2) - h(0))/(1/2 - 0)`

`Rate = (6 - 0)/(1/2 - 0)`

`Rate = (6)/(1/2)`

`Rate =12`

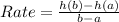
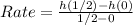
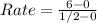
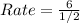
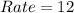
The rate of change is 12ft/s