Question

Write an equation for the line in​ slope-intercept form.

Answer 1

y= -2x +3

Explanation:

What is the slope-intercept form?

• It is when the equation of a line is written as y= mx +c, where m is the gradient (or slope) and c is the y- intercept.

How can we find the equation of a line?

• Two things are needed in order to find the equation of a line, namely

1. Gradient
2. A pair of coordinates (or a point in which the line passes through)

Do note that in the case where the gradient of the line is not stated in the question, it can be obtained using the gradient formula as long as you have two pairs of coordinates. In the formula shown below, (x₁, y₁) is the first pair of coordinates while (x₂, y₂) is the second pair of coordinates.

`\boxed{gradient=(y_1 -y_2)/(x_1 -x_2) }`

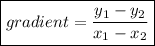
Working to question:

Firstly, let's work out the gradient of the line! In order to do so, we need to identify 2 pairs of coordinates so that we can plug them into the gradient formula.

2 points identified: (0, 3) and (1, 1)

Using the gradient formula,

gradient

`=(3-1)/(0-1)`

`=(2)/(-1)`

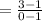
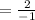
= -2

Substitute the value of the gradient into the equation:

y= -2x +c

c is the y-intercept, which is the y-value in which the line cuts through the y-axis (i.e. occurs at x= 0). Since we have already identified the y-intercept, (0, 3), as one of our points, we can substitute the y-coordinate value into c.

y= -2x +3

In the case where the y-intercept cannot be identified from the graph, you can substitute a pair of coordinates in which the line passes through into the equation after the value of m has been substituted. After solving for c, substitute its value back into the equation and you will arrive at your answer.

y= -2x +c

When x= 1, y= 1,

1= -2(1) +c

1= -2 +c

c= 1 +2

c= 3

Thus, the equation of the line is y= -2x +3.