Question

The length of a rectangle is 4 cm greater than its breadth. if the perimeter of the rectangle is 32cm what is the length and width​

Answer 1

Given :

• The length of a rectangle is 4 cm greater than its breadth. The perimeter of the rectangle is 32cm.

To Find :

• The Length and width of the rectangle.

Solution :

We know that,

`\qquad{ \bold{ \pmb{2(Length + Width) = Perimeter}}}`

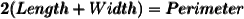
So,

• Let's assume the length of the rectangle as x cm. Then the breadth will become (x – 4) cm.

Now, Substituting the given values in the formula :

`\qquad \dashrightarrow{ \sf{2[x + (x-4)] = 32}}`

`\qquad \dashrightarrow{ \sf{2(x + x-4) = 32}}`

`\qquad \dashrightarrow{ \sf{2(2x-4) = 32}}`

`\qquad \dashrightarrow{ \sf{4x-8= 32}}`

`\qquad \dashrightarrow{ \sf{4x= 32 + 8}}`

`\qquad \dashrightarrow{ \sf{4x= 40}}`

`\qquad \dashrightarrow{ \sf{x= (40)/(4) }}`

`\qquad \dashrightarrow{\pmb{ \bf{x= {10} }}}`

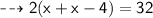
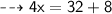
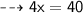
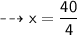
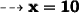
Therefore,

• Length = 10 cm
• Width = (10 – 4) = 6 cm