Question

The measures of the three angles of a

triangle are given by 2x + 6, x, and 3x.
What is the measure of the largest angle?

Answer 1

`\boxed {\boxed {\sf 87 \ degrees}}`

Explanation:

The angles in a triangle must add to 180 degrees.

We are given three angles: 2x+6, x, and 3x. Their sum must be 180, so we can create an equation.

`2x+6+x+3x=180`

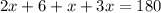
Combine like terms (all terms with an x) on the left side.

`(2x+x+3x)+6=180`

`6x+6=180`

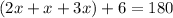
Now solve for x by isolating the variable.

6 is being added and the inverse of addition is subtraction. Subtract 6 from both sides.

`6x+6-6=180-6\\6x=174\\`

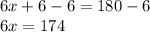
x is being multiplied by 6. The inverse of multiplication is division. Divide both sides by 6.

`6x/6=174/6 \\x=29`

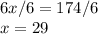
Substitute 29 for x in the angle measures.

• 2x+6= 2(29)+6=58+6=64
• x=29
• 3x= 3(29)=87

The largest angle is 87 degrees.