Question

Determine the graph of the polar equation r = 9/4-4 sin (theta)​

Answer 1

=

7

-

4

Explanation:

=

9

4

−

4

=

−

7

u subtrat ur numbers

Answer 2

To graph the polar equation
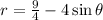`\(r = (9)/(4) - 4 \sin \theta\)`, we can analyze its components.

The equation represents a cardioid, a type of curve in polar coordinates. The key features to note are:

- The coefficient of the
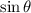`\(\sin \theta\)` term (in this case, -4) determines the number of lobes. Here, it's a single lobe, indicating a cardioid.

- The constant term
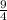`\((9)/(4)\)` represents the distance from the origin to the center of the cardioid.

The graph starts at
`\(\theta = 0\)` and completes one revolution. The radius decreases as
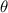`\(\theta\)` increases, forming a heart-shaped curve.

Hence, the complete polar graph of the equation
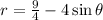`\(r = (9)/(4) - 4 \sin \theta\)` is a cardioid.