Question

`\sf\:Q.\:Show \: that \: there \: is \: no \: positive\:integer`


`\sf\:n \: for \: which \:√(n - 1) \: + \:√(n + 1)\:is`

`\sf\: rational.`​

Answer 1

9514 1404 393

Step-by-step explanation:

We will prove by contradiction. We assume that the given sum is rational, and the ratio can be expressed in reduced form by p/q, where p and q have no common factors.

`√(n-1)+√(n+1)=(p)/(q)\qquad\text{given}\\\\(n-1)+2√((n-1)(n+1))+(n+1)=(p^2)/(q^2)\quad\text{square both sides}\\\\2(n+√(n^2-1))=(p^2)/(q^2)\qquad\text{simplify}`

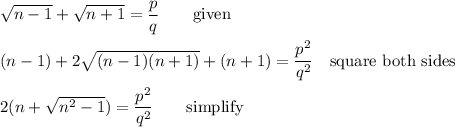
We note that this last equation can have no integer solutions (n, p, q) for a couple of reasons:

1. for any integer n > 1, the root √(n²-1) is irrational (n² is a perfect square; n²-1 cannot be.)
2. p²/q² cannot have a factor of 2, as √2 is irrational

There can be no integer n for which the given expression is rational.